Στο άρθρο αυτό παρουσιάζεται ένα βιντεοσκοπημένο πείραμα που σαν κεντρικό θέμα έχει το φαινόμενο της οριζόντιας βολής, αλλά εμπλέκει και το φαινόμενο της κρούσης δύο όμοιων σφαιρών.
Για το πείραμα χρησιμοποιήθηκαν τα εξής:
- Δύο όμοιες χαλύβδινες σφαίρες διαμέτρου
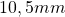και μάζας 
.
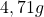- Οδηγός προσαρμοσμένος σε ξύλινη βάση που μπορεί να στηρίζεται σε ορθοστάτη και στον οποίο μπορεί να κυλήσουν οι σφαίρες.
- Κινητό τηλέφωνο με κάμερα λήψης βίντεο στα
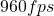, οπότε με αναπαραγωγή στα 
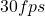η λήψη προβάλλεται σε αργή κίνηση 
. - Κατάλληλη βάση στήριξης στην οποία να μπορεί μόλις να ισορροπεί η μία από τις δύο σφαίρες.
Στην προέκταση του οριζόντιου ευθύγραμμου τμήματος του οδηγού στερεώνεται η μία από τις σφαίρες, πάνω σε κατάλληλη βάση. Η απόσταση από το τέλος του οδηγού μέχρι τη σφαίρα είναι λίγο μεγαλύτερη από την διάμετρο των σφαιρών. Από την κορυφή του οδηγού αφήνεται η δεύτερη σφαίρα, η οποία αμέσως μετά την εγκατάλειψη του οδηγού συγκρούεται κεντρικά με την ακίνητη σφαίρα. Η κρούση είναι με πολύ καλή προσέγγιση ελαστική και οι σφαίρες ανταλλάσσουν ταχύτητες με αποτέλεσμα η αριστερή να ακινητοποιείται στιγμιαία και στη συνέχεια εκτελεί ελεύθερη πτώση, ενώ η δεξιά να εκτελεί οριζόντια βολή.
Δείτε το βίντεο.
Το βίντεο είναι κατάλληλο για επεξεργασία με το πρόγραμμα tracker. Στη συνέχεια παρουσιάζονται τα βασικά σημεία της επεξεργασίας αυτής και τα αποτελέσματά της.
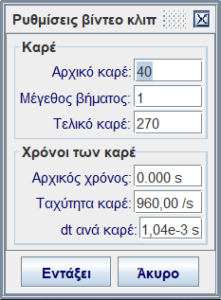
Επιλογή των καρέ του βίντεο που θα αναλύθηκαν και εισαγωγή του ρυθμού δειγματοληψίας ()
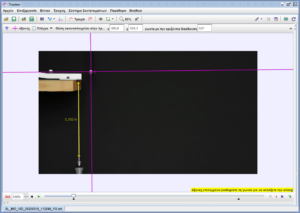
Ορισμός του συστήματος συντεταγμένων, με αρχή την αρχικά ακίνητη σφαίρα και προσανατολισμό των αξόνων με τη βοήθεια του νήματος της στάθμης που είναι προσαρμοσμένο στη τέλος του οδηγού. Πάνω στο νήμα της στάθμης έχουν σημειωθεί δύο σημεία με απόσταση 
τα οποία χρησιμεύουν για την βαθμονόμηση της ράβδου βαθμονόμησης.
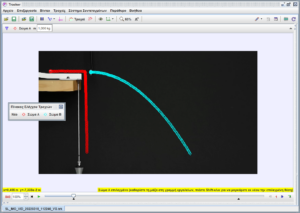
Ορισμός των δύο σφαιρών ως “σώμα Α” την αρχικά κινούμενη στον οδηγό και “σώμα Β” την ακίνητη στην βάση στήριξης. Η ιχνηλασία έγινε αυτόματα και στην εικόνα φαίνονται όλα τα ίχνη.
Η δημιουργία γραφημάτων από το πρόγραμμα και η εισαγωγή των συναρτήσεων προσέγγισης, μας δίνει τη δυνατότητα να μετρήσουμε τις τιμές των χαρακτηριστικών φυσικών μεγεθών κατά τη διάρκεια του φαινομένου.
Από τις μετρήσεις της θέσης στον άξονα x σαν συνάρτηση του χρόνου, μπορούμε να προσδιορίσουμε την οριζόντια ταχύτητα των σφαιρών πριν και μετά την κρούση. Επιλέγουμε τα σημεία που αντιστοιχούν στην κίνηση (είναι τα σημεία των παρακάτω εικόνων που έχουν επισημανθεί με κίτρινο χρώμα), και επιλέγουμε γραμμική συνάρτηση προσέγγισης στην οποία ο συντελεστής του πρωτοβάθμιου όρου είναι η ταχύτητα του σώματος.
Οριζόντια ταχύτητα του σώματος Α πριν την κρούση: 
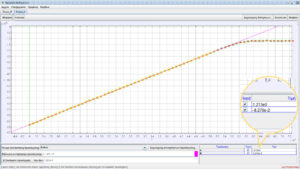
Οριζόντια ταχύτητα της σφαίρας Α μετά την κρούση: 
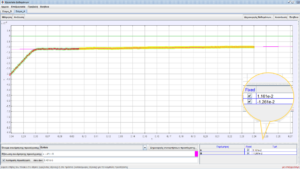
Οριζόντια ταχύτητα της σφαίρας Β μετά την κρούση: 
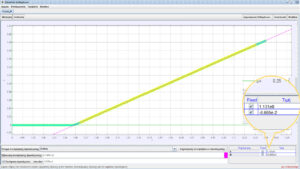
Επιλέγοντας την ανάλυση της κατακόρυφης θέσης σαν συνάρτηση του χρόνου για το σώμα Α βλέπουμε την εξαιρετική συμφωνία των πειραματικών δεδομένων με τη θεωρία η οποία προβλέπει πτώση με σταθερή επιτάχυνση, ίση με την επιτάχυνση της βαρύτητας. Επιλέγοντας καμπύλη προσέγγισης την παραβολή μπορούμε να υπολογίσουμε την τιμή της επιτάχυνσης της βαρύτητας διπλασιάζοντας τον συντελεστή του δευτεροβάθμιου όρου: 
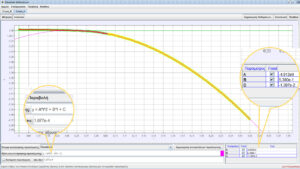
Το πρόγραμμα μας δίνει την πολύ ενδιαφέρουσα δυνατότητα να ορίζουμε σύστημα συντεταγμένων σταθερά προσαρμοσμένο στο σώμα που επιθυμούμε. Στο παρακάτω σχήμα φαίνεται η γραφική παράσταση θέσης χρόνου του σώματος Β στο σύστημα αναφοράς του Α.
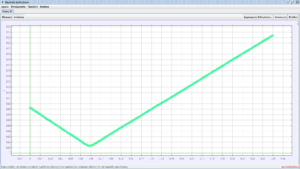
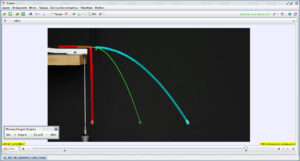
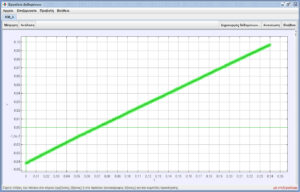
Θεωρώντας τις σφαίρες ως σύστημα σωμάτων, έχουμε τη δυνατότητα να μελετήσουμε την κίνηση του κέντρου μάζας του συστήματος. Στις παρακάτω εικόνες φαίνεται η τροχιά του κέντρου μάζας κατά την εξέλιξη του φαινομένου, καθώς και η γραφική παράσταση της θέσης στον x-άξονα (οριζόντιο) από την οποία συμπεραίνουμε ότι η οριζόντια συνιστώσα της ταχύτητας του κέντρου μάζας παραμένει σταθερή.
Αξιοποιώντας τα στοιχεία που δίνονται, καθώς και τα διαγράμματα που προέκυψαν από την ανάλυση με το tracker, οι μαθητές μπορούν να προσπαθήσουν να απαντήσουν στις προτεινόμενες ερωτήσεις.
- Υπολογίστε την πυκνότητα των σφαιρών.
- Εκτιμήστε την διάμετρο των σφαιρών, αν υποθέσουμε ότι δεν ήταν γνωστή. Αναφέρετε ποιο από τα παραπάνω διαγράμματα χρησιμοποιήσατε και εξηγήστε αναλυτικά το συλλογισμό σας.
- Από το διάγραμμα της θέσης του κέντρου μάζας στον x-άξονα σαν συνάρτηση του χρόνου, υπολογίστε την οριζόντια συνιστώσα της ταχύτητας του κέντρου μάζας. Συγκρίνετέ την με τις αντίστοιχες συνιστώσες των ταχυτήτων των δύο σφαιρών.
- Υπολογίστε την υψομετρική διαφορά αρχικής και τελικής θέσης της σφαίρας που κυλάει στον οδηγό, θεωρώντας δεν ολισθαίνει καθ’ όλη τη διάρκεια της κίνησης (λάβετε υπόψη την παρακάτω φωτογραφία του οδηγού κύλισης).
Μπορείτε να “κατεβάσετε” και να επεξεργαστείτε το αρχικό βίντεο από ΕΔΩ.
Για το πρόγραμμα tracker εκτός από την βοήθεια η οποία περιλαμβάνεται στο μενού του προγράμματος, μπορείτε να “κατεβάσετε” και να μελετήσετε τα παρακάτω εγχειρίδια.
- Από τον κ. Βασίλη Νούση, φυσικό, Υπ. ΕΚΦΕ Θεσπρωτίας, ΕΔΩ.
- Από τον κ. Μιχάλη Πετρόπουλο, φυσικό, Εργαστήριο φυσικής ΕΑΠ, ΕΔΩ
Παρατήρηση:
Η απόκλιση των τιμών των διάφορων φυσικών μεγεθών από τις θεωρητικά αναμενόμενες είναι απολύτως φυσιολογικές και αναμενόμενες. Δεν πρόκειται περί ενός εξιδανικευμένου μοντέλου αλλά για πραγματικό πείραμα με ότι αυτό συνεπάγεται.
Π.χ. η παρατηρούμενη ελάχιστη διαφορά της ταχύτητας της σφαίρας Β μετά την κρούση με την ταχύτητα της Α πριν την κρούση, μπορεί να οφείλεται, (εκτός από τα αναμενόμενα σφάλματα στην διαδικασία βαθμονόμησης και ιχνηλασίας του προγράμματος) στα εξής:
- Η κρούση είναι με πολύ καλή προσέγγιση ελαστική αλλά όχι απολύτως ελαστική (η οποία δεν υπάρχει στον πραγματικό κόσμο).
- Κατά την εκτόξευση της σφαίρας Β υπάρχει μια πολύ μικρή αλλά υπαρκτή αλληλεπίδραση λόγω τριβής με την βάση στην οποία στηρίζεται.